Deviant Syndrome

As a part of me trying to get into DSP (and attract ladies), I made a simple VCV Rack module that does ring modulation. The implementation of this effect in digital domain is devilishly simple. You just multiply two signals sample by sample to get the output. I still wanted my module to comply VCV Rack’s audio audio signal “virtual voltage” standards, so I decided to apply some simple soft clipping to the multiplication product, because multiplication operation can easily give us results in higher orders of magnitude, than the arguments. In theory, a hyperbolic tangent function should applied, because it has those nice smooth leads to the asymptotic (-1, 1). The problem here that it is kinda complex function to evaluate. So, we’d better use some approximation. Let’s see, what is available.

Polynomial interpolation

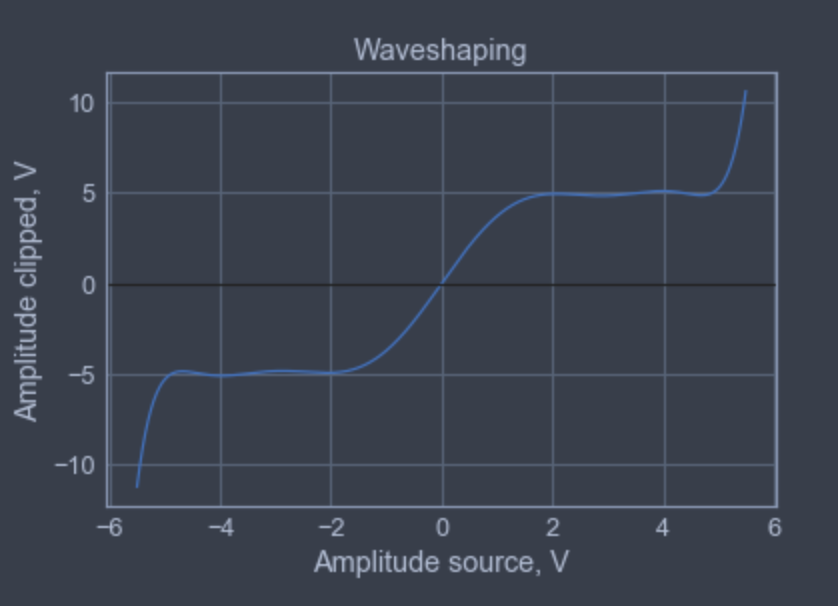
So, we took some of the points of the original curse and interpolated over them. Coefficients are not very important here (or I was too lazy to retype them in \(L_{A}TE^{X}\). Does not look very well to me, it has up to 10th degree argument which implied a lot of multiplications. Also, as you can see from the graph, it goes wild after about, 5. I also tried to experiment to reduce the high-degree arguments as non-significant, but that approach failed miserably. Ok, moving on.

Continued fraction representations

And here we can have a recursive process of getting fractions to achieve a certain degree of approximation. Looks nice, but still quite some work to do, especially in C++ which I’m terrible at. Interesting, can we have a super crude approximation, just giving up on subsequent recursive divisions.

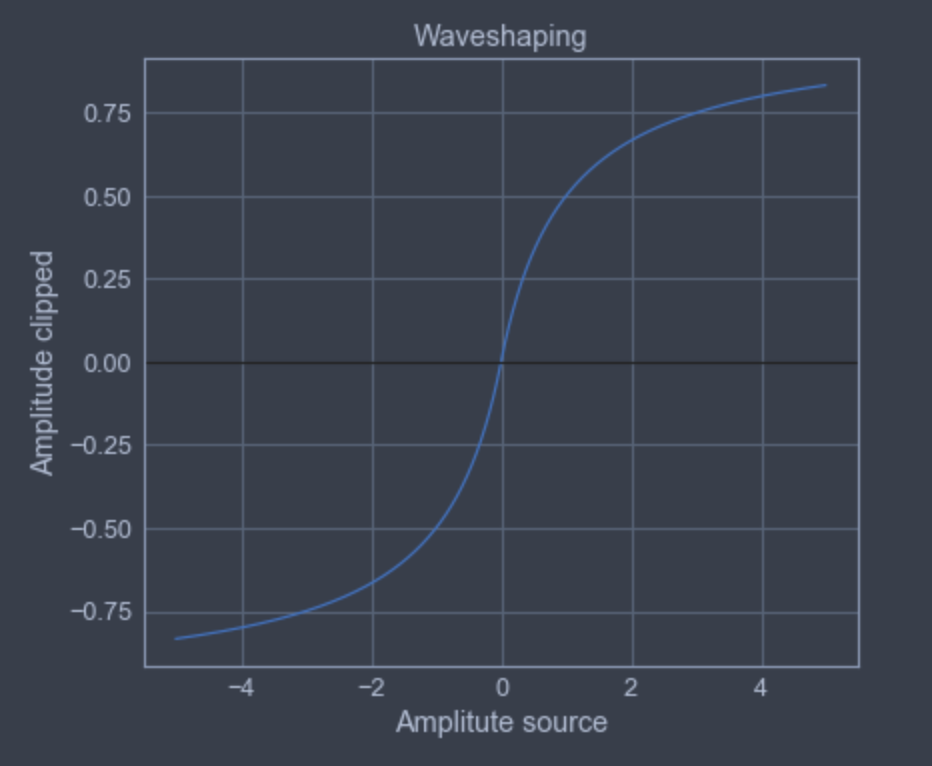
This looks alright, in fact quite suitable for my need of simple output clipping. In case you’re curios, this is how it sounds like:

Two cool guitar licks I’m currently practicing:

(the way I spelled the Coldbound lick would force me to finally start remembering ledger lines. Oh, damn)

Math

As we already know, we can write the Fourier transform in a discrete form like this:

Note, that when working with DFT we use different notation convention. If in a continuous domain we wrote the Fourier transform as \(\hat{f}\), here we notate the sampled (tabbed) function as \(x\) as it’s frequency domain representation as \(X_k\) where \(k\) is the frequency argument.

So, let’s split that heap of sampled function values into two equally sized parts. One part will contain even indexed samples and the other part odd indexed samples, respectively. Then we can rewrite the DFT in the following form:

Now, we want both of this parts to represent a separate self-sufficient DFT transform themselves. To achieve this, we are moving multiplication by 2 from the numerator to denominator, so there it effectively becomes \(N/2\). This way, sigma expression summing from 0 to \(N/2\) becomes a DFT. In the odd part we just moving static stuff outside the sigma operator:

For further convenience we will define left (even) DFT and right (odd) DFT as \(E_k\) and \(O_k\). In this case we can interpret the statement above as:

Now, here is the moment where magic happens: complex exponential functions are periodic, and we can take advantage of that, by reusing already calculated \(E_k\) and \(O_k\) to also calculate \(X_{k + N/2}\). Let’s see, how:

When simplifying this expression, we express exponential degree of sum as a multiplication of two exponential degrees. So, in the first and second sum it just eliminates, because \(e^{-2\pi i m} = 1\) for any \(m\), and the one coefficient on the right will just change it’s sign, because \(e^{-\pi i} = -1\). In detail this would be like:

Which simplifies to:

So, many classical FFT algorithms perform those calculations recursively, reusing the previously computed \(E_k\) and \(O_k\) (which is illustrated by “butterfly” data flow diagram of those algorithms). The complexity of this algorithm family is about O(N log N)

So, I spent a quite a while pimping up my blog engine. And here is the list of awesome features it can do. And event more to come soon. You probably already noticed the cool dark CSS styling of an open-source Jekyll theme, but there is much more to go.

Alright, let’s move.

MathJax support

See the awesome math needed for researching DSP whitepapers and stuff.

AlphaTab sheet music support

I’m struggling to teach myself music theory the most thoughtful way – through understanding written scores and sheet music. There is something about written notations, that makes me feel sorta sophisticated, and as I total narcissist I like that feeling.

AudioJS Embeded MP3 player

Feels super cool to be able to embed my audio demos and sketches with a music player via audioJS. Then they are all nicely sorted Now also with playlist support!

ThebeLab emneded Jupyter notebooks

Python + scipy + numpy inside a Jupyter notebook. There is nothing better to sketch/flesh-out mathematical ideas than that. With [ThebeLab] and a dedicated Jupyter server available, you can make your Python sketches runnable on your site.

%matplotlib inline
import numpy as np
from jupyterthemes import jtplot
import matplotlib.pyplot as plt
jtplot.style()
x = np.linspace(0,10)
plt.plot(x, np.sin(x))
plt.plot(x, np.cos(x))

Coming soon!

• Python notebooks via nbsphinx
• Embed my demos with a music player via audioJS

Suomalainen sanasto

Partituuri

Suomi-sanakirja

Link to different browser embeddable sheet music engines: here

Why?

My addiction to proper dark/low-contract and outright badass interfaces is well-known and could even considered pathological.by one’s standards. This, alongside with inability to use third-party browser extensions in my company’s laptop (for security reasons) finally led me to start exploring the shocking world of DIY Chrome Extensions.

I did not even bother researching what you need to do, for your Chrome extension to make it to Google’s store facilities, I just wanted something, that works locally, personally for me and does one simple thing: dim the eye melting colours of corporate/enterprise web UIs. Thankfully, adding local dev versions of Chrome extensions is fairly straightforward.

First steps

rottingface@vipernest: ~$ md Darkk
rottingface@vipernest: ~$ cd Darkk
rottingface@vipernest: ~/Darkk$ touch manifest.json

{
    "name" : "Darkk",
    "version" : "1.0",
    "content_scripts": [
        {
            "matches": ["https://github.com/*"],
            "css" : ["css/github-dark.css"]
 
        }
    ],
    "permissions" : [ "activeTab", "webNavigation", "*://*/*" ],
    "description" : "Dark mode for my everyday web",
    "manifest_version" : 2
}

When you go to chrome://extensions URL in your browser and click “Add unpacked”, specifying your extension directory.

The catch

There is always one, isn’t it? Some times, it just does not work. Maybe because of Chrome, maybe because of today’s web pages do too much dynamic DOM manipulations on the way. So, in addition to that, I pretended to be a well-trained JS monkey and came up with a script that inserts a new style DOM element, after web page has loaded.

const url = chrome.runtime.getURL('data/github-dark.css');

fetch(url)
    .then((response) => response.text())
    .then((css) => {
        var head = document.head || document.getElementsByTagName('head')[0],
            style = document.createElement('style');

        head.appendChild(style);

        let prcss = css.replace(/@-moz-document regexp\((.*)\) \{(\n|\r)+/, "");
        style.type = 'text/css';
        if (style.styleSheet){
            // This is required for IE8 and below.
            style.styleSheet.cssText = prcss;
        } else {
            style.appendChild(document.createTextNode(prcss));
        }
    });

Here I wanted just a plain simple thing, apply custom CSS to the page, when the URL matches a pattern specified. Started to develop my in-house Google Chrome extension to adjust some of the WebUI palettes of the services I use every day. Let’s see how easy it goes. I could not really use any third+party extension from the Chrome store ob my working laptop, because of my company’s net security guidelines.

So, I created a simple .manifest file. Added a background script that hooks to a navigation complete element. By the way, simple CSS injections via tabs.injectCSS or “css” in manifest file did not work for some reason. Same went for jQuery (modern browsers almost fully blocking any Cross-Origin or local referencies). Was able to make my way simply through creating a style DOM element and filling its gut with my custom CSS content.